[4주차 - norm , inner products, lengths and distance]

norm 

어떤 값의 크기를 계산하여, 비교가 가능하게끔 하는 어떤 함수? 같은 것임. 

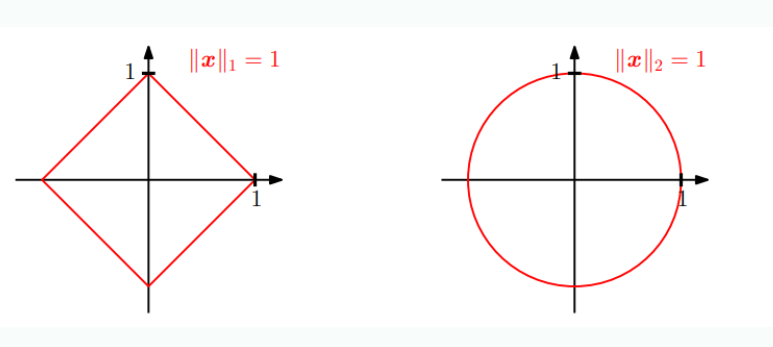
l1 norm (Mahattn distance) 

두개의 벡터를 빼고 , 절대값을 취한뒤 합하는 것 

 

l2 norm (euclidean distance) 

두 개의 각 원소를 빼고 , 제곱하고, 합치고 루트를 씌운것 (두 개 벡터 사이의 직선거리를 말함) 

 

&&교재에서는 특별한 언급이 없다면 euclidean norm을 사용함&&

 

inner Product 

내적은 벡터의 길이나 두벡터 간의 각도 또는 거리 등과 같은 직관 적인 기하학적 개념을 도입하기 위한 것이며 , 

내적의 주요 목적은 벡터가 서로 직교 인지 확인 하는 것이다. 

 

dot product

 

general inner product

두 인자에 대한  mapping 이며, 각 인자에 대해 linear 하다. 

 

symmetric , positive definite matrics 

V xV => R 인 n- 차원  vector space V와 V의 order basis B= (b1,...,bn)가 있다고 가정하면 

x와 y는 다음과  같이 나타낼 수 있다. 

 

 inner product의 biinearity 때문에 모든 x,y 에 대해 성립하게 됨. 

따라서 inner product는 A를 통해 유일하게 결정됨. 

inner product가 symmetry이므로  A도 symmetric 함 

positive definiteness 이므로 

 

 

 

lengths and distances 

 

내적을 통해 norm을 유도 할 수 는 있지만 , 모든 norm이 내적에 의해 유도되는 것은 아니다. 

 

이때 metric 은 다음을 만족한다. 

1.d(x,y) = d(y,x)이다

2.d(x,y)>= 0이고 d(x,y) = 0 <=> x=y 이다. 

3.d(x,z) <= d(x,y) + d(y,z) 이다.