CH03. Regression
| Version | Updated |
| regression with ada 수업 | 2024.07.17 |
| Bias- Variance 추가 , 모델 성능향상 (다중공선성, feature scaling, one hot encoding) |
2024.07.18 |
Regression 이란?
==> 독립변수와 종속변수의 관계를 컴퓨터나 수학적 기술을 사용해서 모델링을 하는 것
Regrssion algorithms의 목표
=> 독립변수의 값을 토대로 종목 변수의 연속 값을 예측하는 것
=> 종변 변수 예측을 위한 독립변수의 회귀 상관 수를 최적화 하는 것

(Linear ) Regrssion Algorithms
1. Linear regrssion ( 선형 회귀)
2. Polynomial regression( 다항 회귀)
3. Ridge regression (릿지 회귀)
4. Lasso regression (라쏘 회귀)
5. ElasticNet regression ( 엘라스틱넷 회귀)
Regrssion Evaluation Metrics
1) MAE(Mean Absolute Error)

실제값과 예측값의 차이의 절대값
특징 : 이상치에 robust함
각각의 error에 대한 기여치가 동일함
2) MSE(Mean Squared Error)

실제값과 예측값의 차이의 제곱값
특징 : MSE에 비해 이상치에 민감함( 에러를 더 크게 만드므로)
편차가 큰 이상값은 MSE를 부풀릴 수 있음.
3) RMSE(Root Mean Squared Error)

실제값과 예측값의 차이의 제곱의 제곱근값
특징: 낮은 RMSE 값일 수록 모델의 성능이 좋다는 것이고, RMSE의 지표가 0이면 완벽한 예측을 뜻함.
RMSE는 MSE보다 이상값에서 덜 민감함.
4) R2 (R-squared)
회귀모델에서 독립 분포로부터 예측할만한 종속변수의 분포를 나타내는것

실제값에서 평균을 뺀것의 제곱 = SST
예측값에서 평균을 뺀것의 제곱 = SSR
실제값에서 예측값을 뺀것의 제곱 =SSE (SSR과 SSE는 어디서 말하느냐에 따라 다 다름)
0은 종속 변수가 모델을 설명하지 않는 것을 뜻함.
1은 종속 변수가 모든 다양성을 다 설명하는 것을 뜻함.
interpretabilty(해석가능성) : 종속변수의 가변성을 모델이 잘 설명하는 지표를 나타냄
sample size의 크기에 덜 민감햠 .
### 주의점
독립변수를 추가하면 R2값이 증가하는 경우가 발생됨.
(독립 변수를 추가할때 모델은 종속변수의 가변성을 더 잘 설명하므로 (SSE값이 작아짐))
모델의 overfitting의 증가 가능성이 있음.
모델 복잡성에 대한 패널티를 주기위해서 adjusted R2 값을 사용하기 도함.

1. Linear Regression
=> 독립변수와 종속변수간의 선형 관계를 모델링 하는 것임.
- simple linear regression (단변량) 단순 선형회귀
- Multiple linear regression (단변량) 다중 선형 회귀
1) OLS (ordinary least squares)
예측값과 실제 값의 차이의 제곱의 합을 나타냄



2. Polynomial Regression
=> polynomial funcition이로서의 종속변수와 독립변수간의 차이를 나타내는 것임.
특징 : polynomial regression은 curve된 데이터를 맞춰주며, 직선을 나타내기 어려울때 변수의 관계를 나타내기 유용하 다.
NORM
==> norm은 벡터공간의 벡터 사이즈 거리등을 할당하는 것이다.

L1 norm이 L2norm 보다 이상치에 강건함.
3. Ridge Regression
==> OLS 선형 회귀 모델에서 오버피팅을 방지 하기 위해 만들어진 모델 이다.

Ridge의 목적은 coefficinet vector( w)값을 최소화하는 것이 목표입니다.

계수의 크기에 페널티를 주어서 보이지 않은 데이터에 대한 일반화를 향상시키고 모델의 안정성을 돕는 것임.
a 즉, lamda는 정규화의 계수에 페널티를 주는 함수임.
4.Lasso Regression
==> Ridge와 마찬가지로 OLS 선형 회귀모델에서 오버피팅을 방지 하기 위해 만들어진 모델이다.


a(alpha or lambda )는 정규화ㅇ 파라비터로 정규화를 얼마나 할지 결정하는 것임.
lasso는 큰 수의 계수에 페널티를 부과하므로써 몇 개의 계수들을 0으로 만들수도 있음 ( feature selection)이 가능 해짐.
Ridge regression VS Lasso Regression
Ridge
- Ridge는 어떤 변수도 0으로 만들지 못함.
-모든 독립변수들이 비슷한 설명력을 가질 때 사용하기 유리함.
LASSO
- Lasso는 어떤 변수를 0으로 만들 수 잇음 .
- 일부 독립변수는 강한 영향을 미치고 일부 독립변수는 영향을 거의 미치지 못할 때 사용함.
5. ElasticNet Regrssion
Lasso와 RIgde를 모두 합친 것임.
두개를 단톡으로 사용 할때 보다 다중공선성 문제에 더욱 더 강건 함.

Bias-Variance Trade-off
모델의 복잡성과 정확성간에 밸런스를 유지하는 것이 좋음.
그래서 bais와 variance 둘다 최소화 하는 방향으로 가야함!!
Bias
- bias는 모델의 평균에서 얼마나 벗어나는지에 대해서 알려주는 것임,
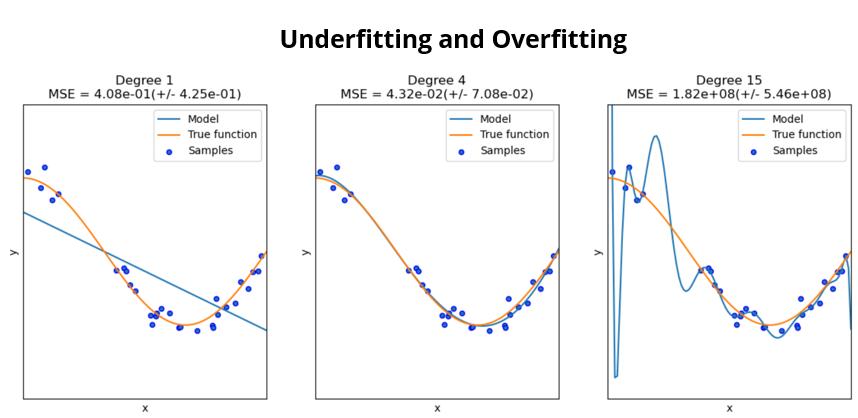
- bias가 높게 되면 underfitting을 유발함 .
Variance
- Variance는 다른 데이터 셋을 모델이 얼마나 잘 측정 하냐를 판단 하는 것임.
- 높은 Variance가 일어나면 모델이 너무 복잡해져서 overfitting이 일어나게 됨.

선형 회귀의 가정
1. 선형성(Linearity)
독립 변수와 종속 변수 사이의 관계가 선형이어야 한다.
2. 독립성 (independence)
오차들 사이에 상관관계가 없어야 한다. 각 데이터 포인트의 오차는 다른 데이터 포인트의 오차와 독립적이어야 한다.
3. 등분산성(Homoscedasticity)
오차의 분산이 모든 독립 변수 수준에서 일정해야 한다. 즉, 예측값의 크기에 상관없이 오차의 분포가 일정하게 유지되어야 한다.
4. 정규성(Normality)
오차는 정규 분포를 따라야 한다. 즉, 오차들이 평균이 0이고 일정한 분산을 가지는 정규 분포를 따라야 한다.
선형 회귀의 제한점
- 이상치에 민감하다.
- 적절한 크기의 데이터 구조가 있으면 underfitting 이 일어날 수 있다.
- 복잡한 모델의 경우 overfitting이 일어날 수 있다.
모델의 성능 향상하기 위한 방법
multicollinearity (다중 공선성) 다루기
Feature Scaling
One-hot Encoding(for categorical variables)
다중 공선성( multicollinearity)
독립 변수들이 서로가 각각 연관이 있을 때 일어나게 됨.
-회귀 계수가 불안정하게 추정될 수 있다.
- 모델을 해석하는데 어려움을 겪을 수 도 있다.
-모델의 예측 정확도를 줄일 수 있다.
*** 다중 공선성을 감지 하는 방법***
1) correlation coefficient : 상관 계수
두 변수간의 선형 관계 ( -1 ~ 1) 이어야 한다.
2) Variance Inflation Factor(VIF): 분산 팽창 지수
특정 독립변수의 계수로 인해서 다른 독립변수가 얼마나 변하는지 측정하는 것.
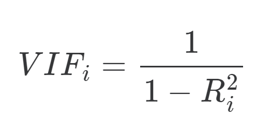
R2 의 경우 (Xhour= aXdays + bXminutes +C) 로 xi 계수를 구하며 OLS 회귀를 사용해서 R2값을 구하게 됩니다.
VIF=1 이면 독립변수와 다른 변수들간에 상관이 없나는 거시고
VIF >=10(5)이상이면 다중 공산성의 문제가 있다는 것으로확인 할 수 있고, 잠재적으로 통계테스트에서 문제가 있을 수 있다는 것을 말 함.
분산 팽창 지수는 특정 독립 변수의 분산이 다른 독립 변수들로 인해 얼마나 팽창하는지를 나타내는 지표로, 다중공선성을 측정하는 데 사용된다.
%correlation Coefficeint %
- 상관 계수는 두 변수 간의 직접적인 선형 관계를 측정하는 반면, VIF는 하나의 변수가 나머지 변수들과의 다중공선성 정도를 측정합니다.
- 상관 계수가 낮다는 것은 두 변수 간의 선형 관계가 약하다는 것을 의미하지만, 이는 다중공선성이 없음을 보장하지 않습니다.
즉, 상관계수가 낮더라도 VIF가높을 수도 있게 되는 것임.
3) Tolerance : 공차 한계
다른 독립변수에 의해 다른 독립변수가 나타나지 않는 지 나타내는것. ( VIF의 역수)

높은 값이면 상관관계가 그렇게 크지 않다는 것이고
낮은 값이면 변수들간의 상관관계가 클 수도 있다는 것이다.
다중 공선성을 다루는 방법
1) Removing variables
높은 상관관계를 보이는 변수 중의 하나를 제거하는 것이다.
but, 높은 상관 관계를 보이면서 모델의 방향에 큰 영향을 미치지 않더라도, 잠재적으로 영향을 미칠 수 있기 때문에
제거하기전에 꼼꼼히 따져보고 제거 해야한다.
2) combinig variables
- Sum or Average
두개의 요소를 결합하는 것이다.
- Principal Component Analysis(PCA)
데이터의 분산은 보유하는 동안 데이터 셋의 차원을 줄이는 방법이다.
이것은 주성분(PC)로 알려진 상관되지 않은 세로운 변수로 바꿔주는 것임.
3) Regularization
ridge나 Lasso를 활용해서 정규화를 시켜줌 ( 특히 lambda 값을 변형해가면서)
Feature Scaling
feature scaling은 변수의 범위를 조정하는 과정을 나타내는 것임. 비슷한 크기를 나타내기 위해서
1) Standardization(표준화)
평균이 0이고 표준편차가 1인 것으로 만드는 것임.
이상치에 강건하며 , 데이터가 정상 분포를 따를때 적절하다.

2) Normalization(정규화)
feature의 범위를 0에서 1로 변환하는 것임.

One hot Encoding
원-핫 인코딩은 범주형 변수를 이진 형태로 변환해서 나타내는 것을 말함.
이때 다중 공선성 문제 때문에 하나를 삭제 해야함.
