CH04 . 3-4 cholesky decompostion , eigendecompostion and diagonalization

Cholesky Decomposition 

 

머신러닝에서는 행렬을 특별한 타입으로 분해하는 여러 방법들을 사용한다. Positive read number에서는 숫자를 동일한 구성요소로 분해하는 제곱근과 같은 연산이 있다. 

행렬의 경우에는 양수에 대해 제곱근과 같은 연산을 할때 주의해야한다. 

 

대칭이면서 positive definite(양의 정부호)인 행렬의 경우, 여러 square-root equivalent operations 중 선택할 수 있다. 

cholesky decompostion/ cholesky factorization 

 

 

 

 

nultivariate Gaussian variable (다변량 가우시안 변수)의 covariance matrix(공분산 행렬)는 symmetric, positive definite 하다.  이 공분산 행렬의 cholesky factorization은 가우시안 분포로부터 샘플을 생성하도록 한다. 

 

또한 VAE 와 같은 deep stochastic modl 에서 기울기를 계산 할 때 많이 사용되는 확률 변수의 linear transformation을 수행 할 수 있도록 한다. 

 

cholesky decomposition 을 통해 determinant를 매우 효율적으로 계산 할 수 있다\

 

 

Eigendecompostion and diagonalization 

 

diagonal matrix는 대각행렬이라고 하며 대각 성분이 아닌 요소들이 모두 0인 행렬이다. 

대각 행렬에서는 determinants(행렬식), power(거듭제곱), inverse(역행렬) 를 빠르게 계산 할 수 있다. 

대각 행렬의 곱은 대각 성분들을 k 거듭제곱하면 된다. 

 

행렬 A를 대각화하는 것은 다른 baisis의 동일한 linear mapping 이며, 이 basis는 결국 A의 eigenvector로 구성되어 있다는 것을 확인합니다. 

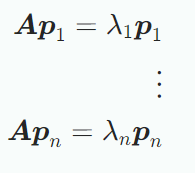
따라서 P의 column들은 반드시 A의 eigenvectors이다. 

 

Diagonalization 

행렬 P가 invertible 하다는 것을 필요로 하다. P는 full rank이어야 한다. 

n 개의 linearly indepedent eigenvectors p1, ..., pn을 요구하는 것이며, 따라서, 

pi는 basis를 형성한다. 

non-defective matrix만 대각화할 수 있다는 것과 P의 column들은 A의 n개의 eigenvectors라는 것을 함시한다. 

 

행렬 A를 standard basis에 대한 linear mapping 의 transformation matrix라고 한다. p-1은 standard basis에서 eigenbasis 로의 basis change를 수행한다. 이는 eigenvectors pi를 standard basis vectors ei로 만든다. 그리고 , 대각행렬 D는 eigenvectors Pi를 standard bsis vectors ei로 만든다.  그리고 , 대각행렬 D는 eigenvalues 만큼 축을 따라 크케일링한다. 

마지막으로 P는 sclaing 된 벡터들을 다시 standard /canonical coordinates로 변환한다. 

 

 

 

참고블로그  

https://junstar92.github.io/mml-study-note/2022/07/14/ch4-3.html

 

https://junstar92.github.io/mml-study-note/2022/07/15/ch4-4.html